决策树回归

回归

使用类DecisionTreeRegressor, 决策树可以应用于回归问题。fit方法取输入数组X, y, 这里的y取浮点值而不是分类的整值。

1 from sklearn import tree

2 X = [[0, 0], [2, 2]]

3 y = [0.5, 2.5]

4 clf = tree.DecisionTreeRegressor()

5 clf = clf.fit(X, y)

6 clf.predict([[1, 1]])

复杂度

通常，构建一棵平衡的二值树的运行时间代价是 O(n_samplesn_featureslogn_samples), 查询时间是 O(logn_samples). 尽管建树算法试图产生平衡的树，但结果树并不总是平衡的。假设子树维持大致的平衡，在每一个节点的代价包括搜遍 O(n_features) 到找到提供最大熵减少量的特征。在每个节点的代价 O(n_featuresn_sampleslogn_samples), 这样，加和所有节点的代价得到整棵树的总的代价是 O(n_featuresn²_sampleslogn_samples).

Scikit-learn提供了更加有效的决策树构建执行。一个naive执行是，重新计算类标签直方图（分类问题），或者沿着一个给定的特征，在每个新分割点的均值（回归问题）。在所有相关的样本上预先排序特征，保持一个运行标签计数，将减少每个节点的复杂度到 O(n_featureslogn_samples), 这样，整个代价是 O(n_samplesn_featureslogn_samples). 这是一个基于所有树算法的选项。

实际使用提示

对于包括大量特征的数据，决策树容易过度拟合数据。得到样本与特征的比率是重要的，因为高维空间、小样本的树很容易是过度拟合的。

在建树前可以考虑作特征降维（PCA, ICA, 特征选择）。

使用export函数可视化树，使用参数max_depth=3作为一个初始的树深度，对树拟合数据的程度有一个初步的感觉，然后再增加树深。使用max_depth控制树的规模，避免过度拟合。

使用min_samples_split or min_samples_leaf控制每个叶子节点的样本数。样本量太少通常意味着过度拟合，而样本量太大会抑制树从数据学习。试设min_samples_leaf=5作为初始值，如果样本量变化很大，一个浮点数可以作为这两个参数的百分比。它们之间的区别是，min_samples_leaf保证了在叶子的最小样本量，而min_samples_split能产生任意小的叶子，min_samples_split在文献里是更普遍使用的。

在训练前平衡你的数据集，避免树偏向于占支配地位的类。类平衡可以通过从每个类中抽取等量的样本实现，更好的做法是，规范化每一个类的样本权和到相同的值。

如果样本加权了，那么，使用基于权的预修剪准则，例如，min_weight_fraction_leaf, 更容易优化树结构。

所有的树都使用了np.float32数组。如果训练数据并不是这种格式，将作一个数据集拷贝。

如果输入矩阵X是稀疏的，建议拟合前转换到稀疏的csc_matrix, 预测前转换到稀疏的csr_matrix. 当特征在大多数样本里是0时，在稀疏输入矩阵上的训练时间要更快一些。

树算法

ID3(Iterative Dichotomiser 3)算法产生一棵多叉树，在每一个节点寻找产生类目标的最大信息增益的类特征。树生长到最大的规模，然后通常应用一个修剪步，改善树的预测能力。

C4.5算法是ID3算法的继承，去掉了对特征必须是类别的限制。它根据数值变量，动态地定义一个离散属性，用来分割连续属性值为一个离散的区间集。C4.5转换训练树（即，ID3算法的输出）为if-then规则集。随后，评价每一个规则的准确性，以此确定规则应用的顺序。

C5.0算法是C4.5的升级版，它使用更少的内存，创建更少的规则，而保持更高的准确性。

CART(Classification and Regression Trees)算法类似于C4.5, 区别在于它支持数值目标变量（回归），并不计算规则集。CART使用特征和阈值创建二值树，阈值在每一个节点产生最大信息增益。scikit-learn实际使用的是一个CART算法的优化版本。

数学原理

给定训练向量 x_i∈Rⁿ, i=1,…,I. 标签向量 y∈R^l, 一棵决策树递归地分割空间，使得具有相同标签的样本被分到一起。

令 Q 表示节点 m 的数据。对于每一个候选分割 θ=(j,t_m), j 表示特征， t_m 表示分割数据 Q 为 Q_left(θ), Q_right(θ) 子集的阈值。其中，

                                               Q_left(θ)=(x,y)/x_j≤t_m

                                               Q_right(θ)=Q∖Q_left(θ)

使用非纯度函数 H() 计算 m 点的不纯度(impurity), H 的选择依赖于要解决的问题的性质（分类还是回归）。 

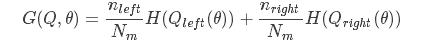
选择使不纯度最小的参数 θ

                                                θ^∗=arg_θminG(Q,θ)

在子集 Q_left(θ^∗),Q_right(θ^∗) 上递归，直到达到最大允许深度， N_m<min{samples} 或者 N_m=1.

分类原则

如果目标是在 0,1,…,K−1 上取值的分类结果。对于节点 m, R_m 表示具有 N_m 个观测的区域，令 

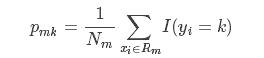
是节点 m 处属于类 k 的观测比例。

表示不纯度，普遍采用的是

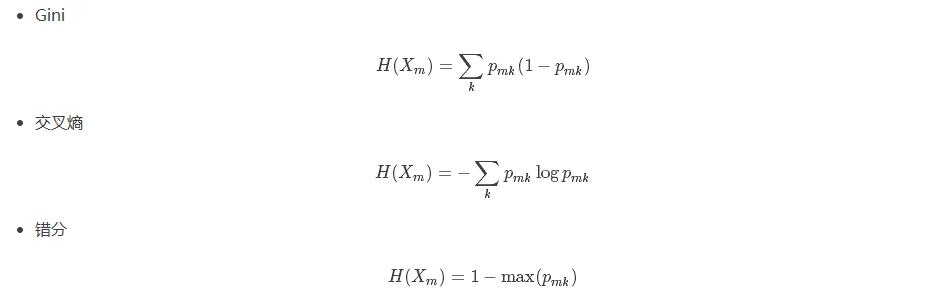
这里， X_m 是节点 m 的训练数据。

回归原则

如果目标变量是连续的，那么对于节点 m, R_m 表示具有 N_m 个观测的区域，确定下一步分割的普遍原则是，最小化均方误差(Mean Squared Error), 即，使用终点的均值，最小化L2误差。或者最小化平均绝对误差(Mean Absolute Error), 即，使用终点的中位数值，最小化L1误差。

这里， X_m 是节点 m 处的训练数据。