域分解机

符号说明：

x表示样本特征数据

y表示样本目标数据

第i个训练样本为(x_i,y_i)，为了方便也可以用x=x_i表示第i个样本

1 基于域的分解机模型（FFM）

1.1 线性模型

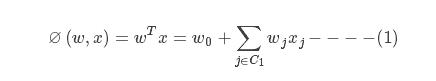
C₁表示x零元素索引的集合

1.2 二次多项式模型

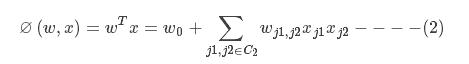
C₂表示x中非零的组合元素索引的集合

1.3 分解机模型

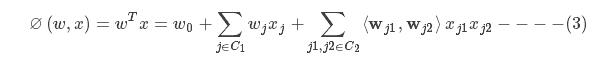
w是二维矩阵，w_i表示第i行向量，长度为k，k是用户自定义的参数，也称之为隐变量

1.4 域分解机模型

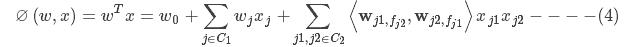
因为线性项

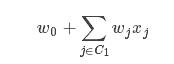
在训练过程中非常容易计算，所以可以先将其忽略，只需要研究

                                           ，

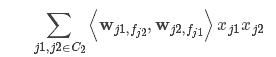将其写成另一种形式

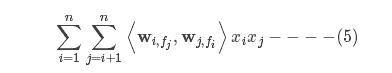
1.5 基于FFM的逻辑回归模型

1.5.1-1，1损失的逻辑回归模型         

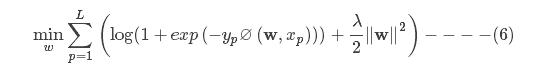
其中

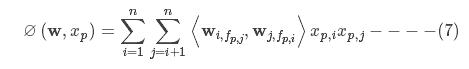
令

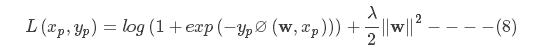
其为每个样本的损失函数。

L(x_p,y_p)对参数w的导数为：

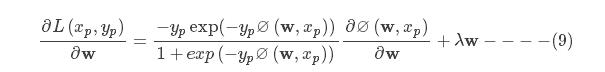
在式（8）的导数计算公式中，

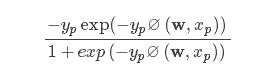
是标量，对于每个样本只要按照式（7）计算即可，第二项

                                                        λw

用惩罚参数乘以对应的参数即可，比较麻烦的就是

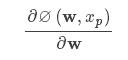
的计算。

1.5.2 ∅(w,x_p)的求导过程$

为了便于理解首先对

⟨                                        

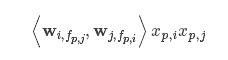
中的

                                                      w_i,fp,j

和

                                                      w_j,fp,i

分别的偏导数如下

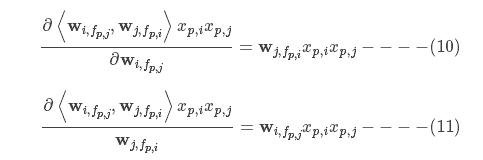
所以∅(w,x_p)对w_i,fp,j和w_j,fp,i的偏导数分别如下

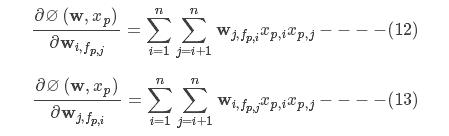
                                    训练模型时需要注意的问题：在式（12）和式（13）中会存在

                                              w_j,fp,i(x_t,ix_t,j+x_q,ix_q,j+⋯)

                                    在训练时不需要合并这些项，只要把这些项当成更新参数

                                                      w_j,fp,i

                                     的多个样本即可，这在编程实现中将非常有用。

假设有如下的例子，五个特征，两个域

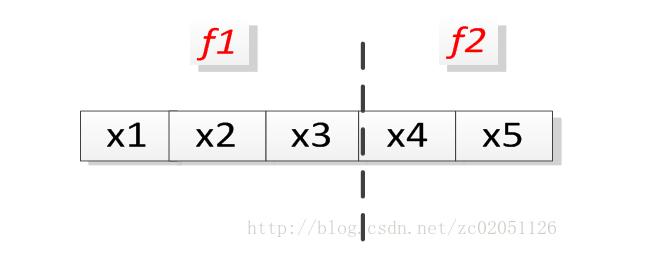
                                                        图1

按照式（7），去掉下标p，计算图1中所示的分解模型，如下按照式（7），去掉下标p，计算图1中所示的分解模型，如下

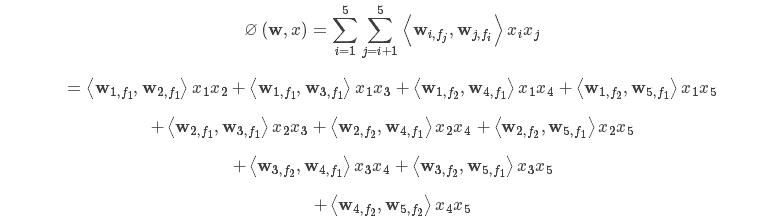
从上式中抽取i=1,f_j=1和i=3,f_j=2

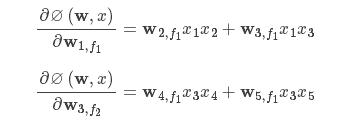
在模型学习时，需要迭代公式

                                                          w=w+ηg，

η,g分别为学习率和梯度向量，则在计算

                                                          w_3,f2

时有两种方式：

方式1：

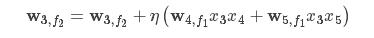
方式2：

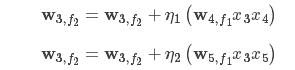
因为采用的是AdaGrad所以学习率η在方式二中是变化的。因为采用的是AdaGrad所以学习率η在方式二中是变化的。

在学习过程中是采用方式1还是方式2呢？答案是方式2。因为在计算实际问题时可能特征分布在多个域中，如果按照方式1则需要把每个域中的信息累加起来，结果是编程上非常麻烦，如果按照方式2，非常符合SGD的思想，把w_4,f1x3x4和w_5,f1x3x5看成两个样本，再带回到x3x4x3x4组合时更新下w_3,f2，当访问到x3x5x3x5组合时再次更新下w_3,f2，在实际编程中，具体更新哪些参数可以通过相应的索引进行访问，非常方便。