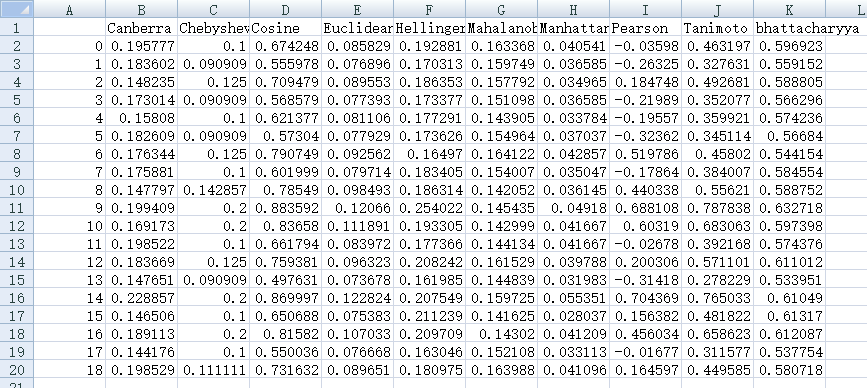
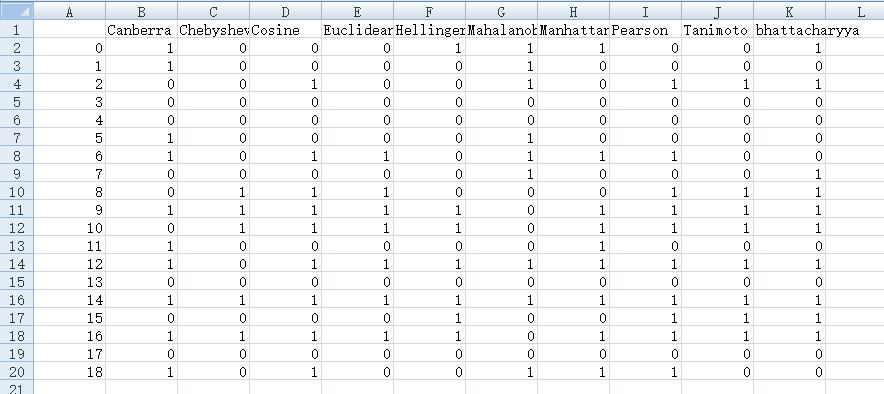
Related Info
:Manhattan Distance
:Euclidean Distance
:Chebyshev Distance
要求样本数要大于维数,否则无法求协方差矩阵
有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为:
其中向量之间的马氏距离定义为:
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了欧式距离:
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
是类别数,
是第i类的概率
相似系数
杰卡德距离
f-divergence Distance
如果P和Q被定义成空间中的两个概率分布,则f散度被定义为:
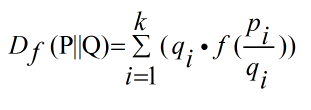
一些通用的散度,如KL-divergence, Hellinger distance, 和total variation distance,都是f散度的一种特例。只是f函数的取值不同而也。

Hellinger Distance
1 定义
1.1 度量理论
为了从度量理论的角度定义Hellinger距离,我们假设P和Q是两个概率测度,并且它们对于第三个概率测度λ来说是绝对连续的,则P和Q的Hellinger距离的平方被定义如下:
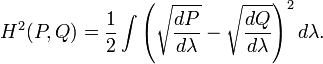
这里的dP / dλ 和 dQ / dλ分别是P和Q的Radon–Nikodym微分。这里的定义是与λ无关的,因此当我们用另外一个概率测度替换λ时,只要P和Q关于它绝对连续,那么上式就不变。为了简单起见,我们通常把上式改写为:
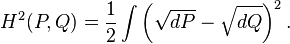
1.2 基于Lebesgue度量的概率理论
为了在经典的概率论框架下定义Hellinger距离,我们通常将λ定义为Lebesgue度量,此时dP / dλ 和 dQ / dλ就变为了我们通常所说的概率密度函数。如果我们把上述概率密度函数分别表示为 f 和 g ,那么可以用以下的积分形式表示Hellinger距离:
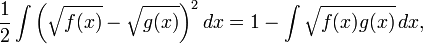
上述等式可以通过展开平方项得到,注意到任何概率密度函数在其定义域上的积分为1。
根据柯西-施瓦茨不等式(Cauchy-Schwarz inequality),Hellinger距离满足如下性质:
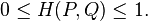
1.3 离散概率分布
对于两个离散概率分布 P=(p1,p2,...,pn)和 Q=(q1,q2,...,qn),它们的Hellinger距离可以定义如下:
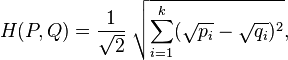
上式可以被看作两个离散概率分布平方根向量的欧式距离,如下所示:
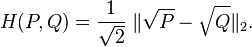
也可以写成:
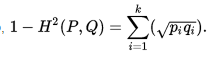
在统计中,Bhattacharyya距离测量两个离散或连续概率分布的相似性。它与衡量两个统计样品或种群之间的重叠量的Bhattacharyya系数密切相关。Bhattacharyya距离和Bhattacharyya系数以20世纪30年代曾在印度统计研究所工作的一个统计学家A. Bhattacharya命名。同时,Bhattacharyya系数可以被用来确定两个样本被认为相对接近的,它是用来测量中的类分类的可分离性。
对于离散概率分布 p和q在同一域 X,巴氏距离被定义为:
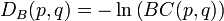
其中BC(p,q)是Bhattacharyya系数:
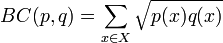
从公式可以看出,Bhattacharyya系数BC(P,Q)可以和前面的Hellinger距离联系起来,此时Hellinger距离可以被定义为:
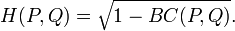
因此,求得巴氏系数之后,就可以求得巴氏距离和Hellinger距离。
Maximum Mean Discrepancy
最大均值差异(Maximum mean discrepancy),度量在再生希尔伯特空间中两个分布的距离,是一种核学习方法。两个随机变量的距离为:
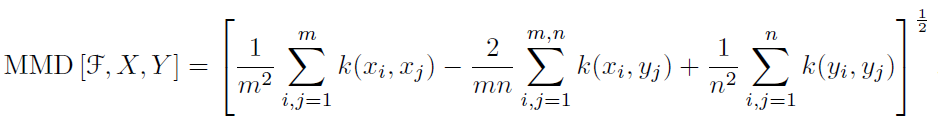
其中k(.)是映射,用于把原变量映射到高维空间中。X,Y表示两种分布的样本,F表示映射函数集。
基于两个分布的样本,通过寻找在样本空间上的映射函数K,求不同分布的样本在K上的函数值的均值,通过把两个均值作差可以得到两个分布对应于K的mean discrepancy。寻找一个K使得这个mean discrepancy有最大值,就得到了MMD。最后取MMD作为检验统计量(test statistic),从而判断两个分布是否相同。如果这个值足够小,就认为两个分布相同,否则就认为它们不相同。更加简单的理解就是:求两堆数据在高维空间中的均值的距离。
近年来,MMD越来越多地应用在迁移学习中。在迁移学习环境下训练集和测试集分别取样自分布p和q,两类样本集不同但相关。我们可以利用深度神经网络的特征变换能力,来做特征空间的变换,直到变换后的特征分布相匹配,这个过程可以是source domain一直变换直到匹配target domain。匹配的度量方式就是MMD。
Wasserstein Distance
Wasserstein 距离,也叫Earth Mover's Distance,推土机距离,简称EMD,用来表示两个分布的相似程度。
Wasserstein distance 衡量了把数据从分布“移动成”分布
时所需要移动的平均距离的最小值(类似于把一堆土从一个形状移动到另一个形状所需要做的功的最小值)
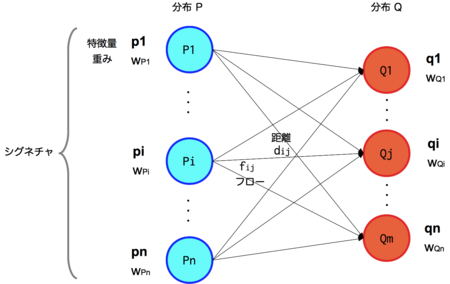
假设有两个工地P和Q,P工地上有m堆土,Q工地上有n个坑,现在要将P工地上的m堆土全部移动到Q工地上的n个坑中,所做的最小的功。
每堆土我们用一个二元组来表示(p,w),p表示土堆的中心,w表示土的数量。则这两个工地可表示为:
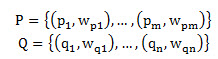
每个土堆中心pi到每个土坑中心qj都会有一个距离dij,则构成了一个m*n的距离矩阵。
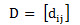
那么问题就是我们希望找到一个流(flow),当然也是个矩阵[fij],每一项fij代表从pi到qj的流动数量,从而最小化整体的代价函数:
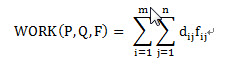
问题描述清楚了:就是把P中的m个坑的土,用最小的代价搬到Q中的n个坑中,pi到qj的两个坑的距离由dij来表示。fij是从pi搬到qj的土的量;dij是pi位置到qj位置的代价(距离)。要最小化WORK工作量。EMD是把这个工作量归一化以后的表达,即除以对fij的求和。
EMD公式: