机器听不懂我们人类语言，我们得用数学语言向它描述问题，这就叫“建模”。

Google 研发了十年自动驾驶后，终于在本月上线了自动驾驶出租车服务。感谢“深度学习”技术，人工智能近年来在自动驾驶、疾病诊断、机器翻译等领域取得史无前例的突破，甚至还搞出了些让人惊艳的“艺术创作”：

AI 生成的奥巴马讲话视频，看得出谁是本尊吗？

开源软件 style2paints 能自动给漫画人物上色

如果不了解其中的原理，你可能会觉得这是黑魔法。

“深度学习”虽然深奥，本质却很简单。无论是图像识别还是语义分析，机器的“学习”能力都来源于同一个算法 — 梯度下降法 (Gradient Descent)。要理解这个算法，你所需要的仅仅是高中数学。希望在读完这篇文章后，你看待 AI 的眼光会改变。

一个例子

我们从一个具体的例子出发：如何训练机器学会预测产品的成品率。在现实中，产品的成品率由很多因素决定。但为了让问题简单点，我们只考虑温度这一个因素。

在机器学习领域，这样的问题被称为“监督学习 (Supervised Learning)”。意思是，如果我们想让机器学会一件事（比如预测产品的成品率），那就给它看很多例子，让它学会举一反三（预测某一温度下成品率是多少）。其实跟人类的学习方法差不多，对吧？

现在假设我们收集了 100批次的成品率，作为给机器学习的例子。大致情况如下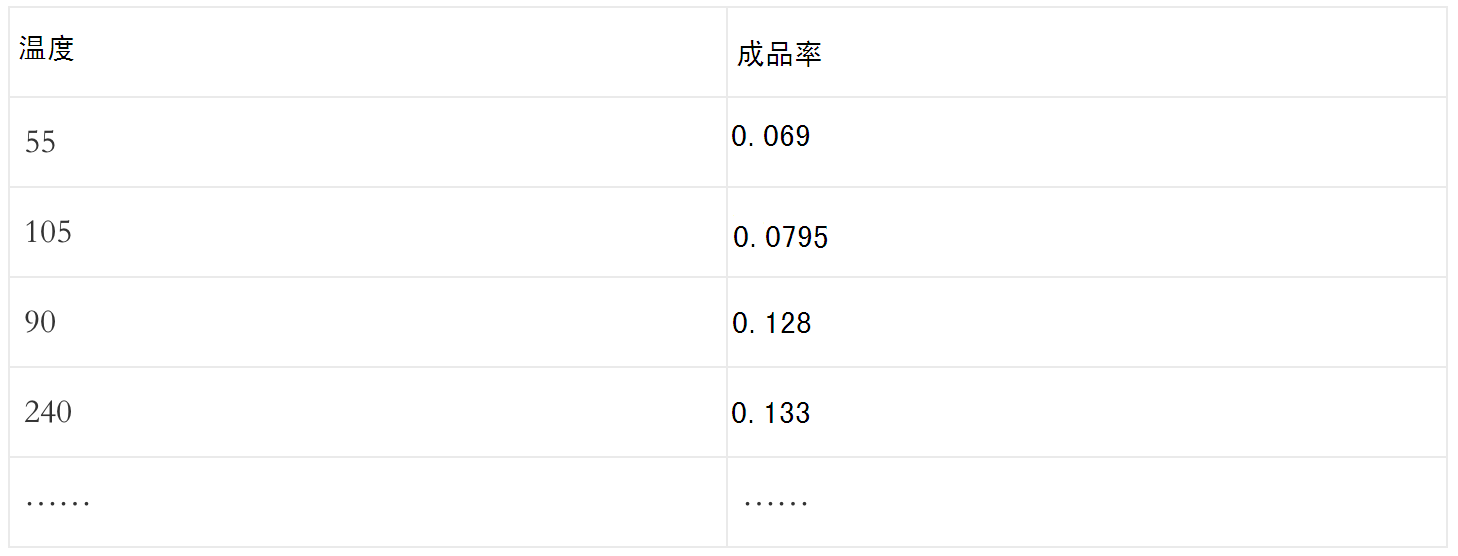：接下来我们要做两件事：

1. 告诉机器该学习什么；

2. 等机器学习。

告诉机器该学什么

为了让机器听懂问题，我们不能说普通话，得用数学语言向它描述问题，这就是所谓的“建模”。为了让接下来的分析更直观，我们把收集回来的例子画在数轴上：

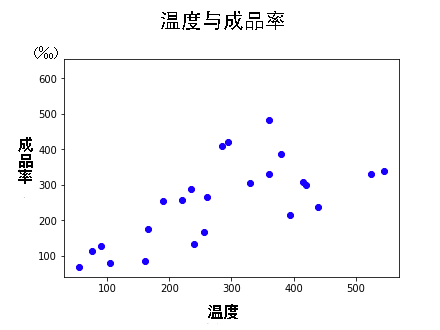
我们希望机器通过这些样本，学会举一反三，当给定某一温度时，能预测成品率。比如说，预测温度为480度时成品率是多少：

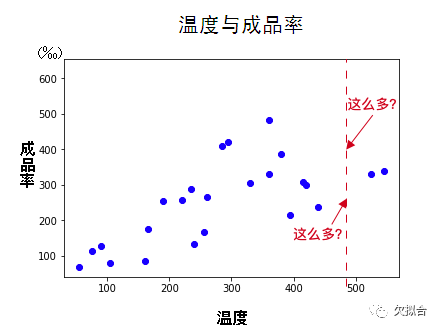
480度的成品率是多少？

观察图表，我们能看出温度和成品率可能大概是线性关系，也就是说，我们可以画一根贯穿样本的直线，作为预测模型。

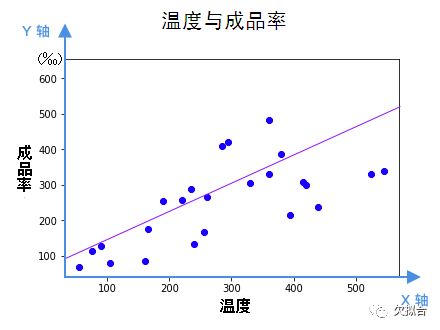
如果我们把温度看作 X 轴，成品率看作 Y 轴，这根直线就可以表示为：

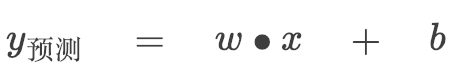
w 决定直线的倾斜程度，b 决定这根直线和 Y 轴相交的位置。问题是，看起来有很多条线都是不错的选择，该选哪条？换句话说 w 和 b 该等于多少呢？

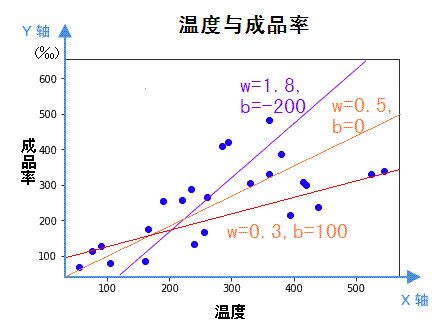
每根直线都是一个候选的模型，该选哪个？

显然，我们希望找到一根直线，它所预测的成品率，跟已知实际数据的误差最小。换句话说，我们希望下图中的所有红线，平均来说越短越好。

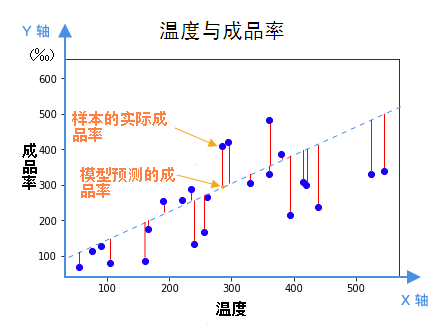
红线的长度，就是我们的模型预测的成品率（蓝色虚线）和实际数据的成品率（蓝点）之间的误差，红线的长度等于预测成品率和实际成品率的差值。以第一个样本（实际数据）为例，温度为55度时，成品率为 69 ‰（千分之69），所以第一根红线的长度等于：

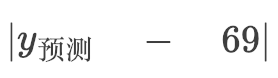
因为绝对值不便于后面的数学推导，我们加个平方，一样能衡量红线的长度。

因为我们的预测模型是：

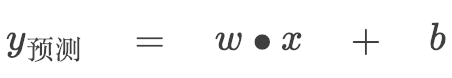
所以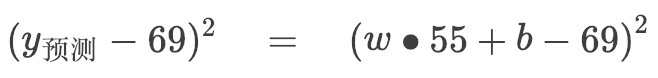
这个样本（实际数据）是温度为55度时成品率为69‰（千分之69）。

算式开始变得越来越长了，不过这只是变量代换而已！前面提到，我们希望所有红线平均来说越短越好，假设我们有 100 个批次，用数学来表达就是：

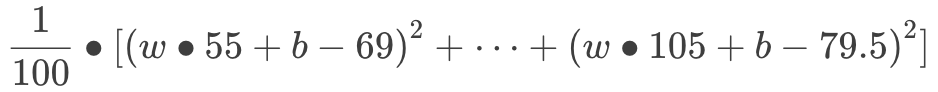
至此，我们把“预测成品率”这个问题翻译成数学语言：“找出 w 和 b 的值，使得以上算式的值最小。”坚持住，第一步马上结束了！

我们现在有 2 个未知数：w 和 b。为了让问题简单一点，我们假设 b 的最佳答案是 0 好了，现在，我们只需要关注 w 这一个未知数：

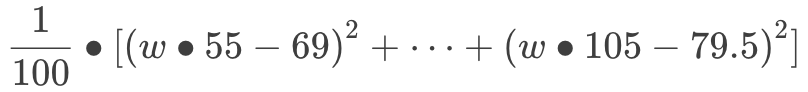
把括号打开：

在机器学习领域，这个方程被称为“代价 (cost) 函数”，用于衡量模型的预测值和实际情况的误差。我们把括号全打开：

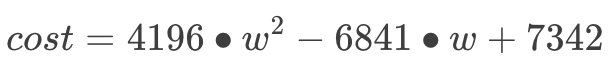
（不用在意方程中的数字，由于100批次的数据计算量大，就随便写了几个）

至此，我们把“预测成品率”这个问题翻译成数学语言：“w 等于多少时，代价函数最小？”第一步完成！到目前为止，我们只用上了直线函数。

机器是怎么学习的

代价函数是个一元二次方程，画成图表的话，大概会是这样：

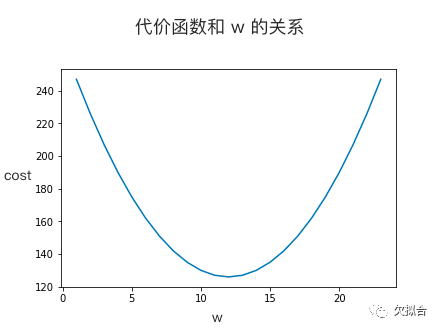
（不用在意坐标轴上的具体数字，也都是随便写的）

前面讲到，机器要找到一个 w 值，把代价降到最低：

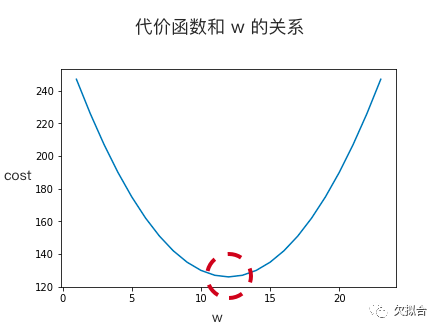
机器采取的策略很简单，先随便猜一个答案（比如说 w 等于 20 ，下图红点），虽然对应的代价很高，但没关系，机器会用“梯度下降法”不断改进猜测。

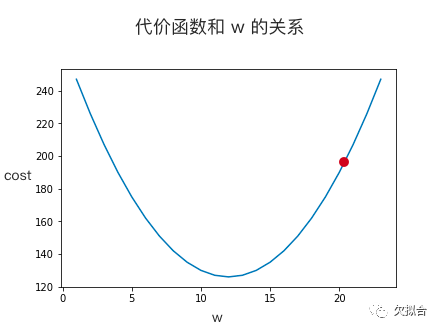
如果你微积分学得很好，此时可能会问：求出导数函数为 0 的解不就完事了吗？在实际问题中，模型往往包含上百万个参数，它们之间也并非简单的线性关系。针对它们求解，在算力上是不现实的。

现在，我们得用上另一个函数——求导函数了。针对这个随便猜的点求导，导数值会告诉机器它猜得怎么样，小了还是大了。

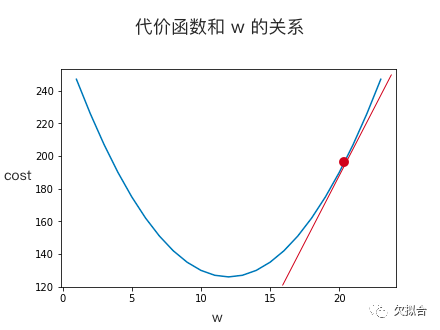
如果你不记得导数是什么，那就理解为我们要找到一根直线，它和这条曲线只在这一个点上擦肩而过，此前以后，都无交集。所谓的导数就是这根线的斜率。

【导数是微积分中的重要基础概念。当函数y=f(x)的自变量X在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0)或df/dx(x0)。】

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。

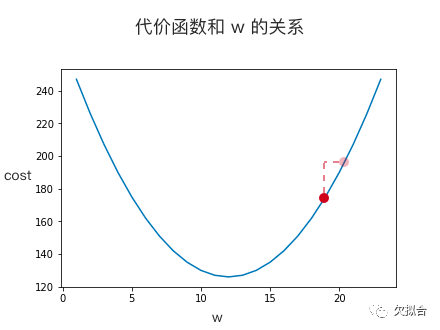
我们可以看得出，在代价函数的最小值处（即曲线的底部）导数等于 0。如果机器猜测的点，导数大于 0，说明猜太大了，下次得猜小一点，反之亦然。根据导数给出的反馈，机器不断优化对 w 的猜测。因为机器一开始预测的点导数大于 0 ，所以接下来机器会猜测一个小一点的数：

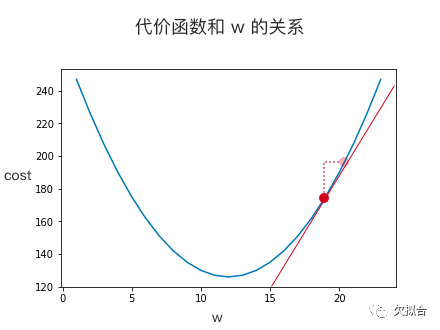
机器接着对新猜测的点求导，导数不等于 0 ，说明还没到达曲线底部。

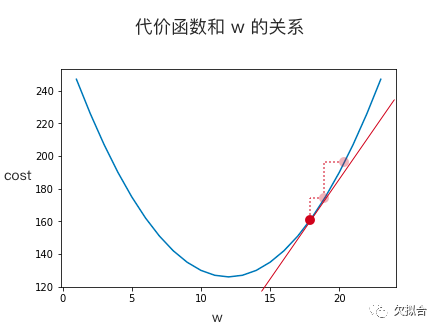
那就接着猜！机器孜孜不倦地循环着“求导 – 改进猜测 – 求导 – 改进猜测”的自我优化逻辑 —— 没错，这就是机器的“学习”方式。顺便说一句，看看下图你就明白它为什么叫做“梯度下降法”了。

终于，皇天不负有心机器，机器猜到了最佳答案：

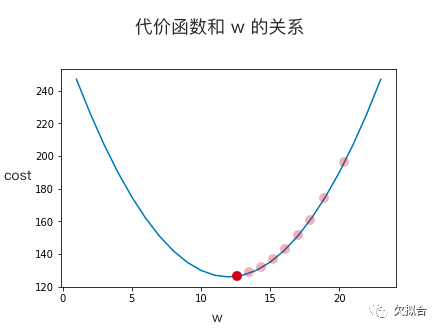
就这样，头脑简单一根筋的机器靠着“梯度下降”这一招鲜找到了最佳的 w 值，把代价函数降到最低值，找到了最接近现实的完美拟合点。

总结一下，我们刚刚谈论了三件事：

1. 通过观察数据，我们发现页数与书价是线性关系——这就是选定模型；

2. 于是我们设计出代价函数，用来衡量模型的预测成品率和已知样本（实际数据）之间的差距——告诉计算机该学习什么；

3. 机器用“梯度下降法”下，找到了把代价函数降到最低的参数 w ——机器的学习方法。

机器“深度学习”的基本原理就是这么简单。现在请思考一个问题：机器通过这种方法学到的“知识”是什么？

现实问题中的深度学习

为了让数学推演简单点，用了一个极度简化的例子。现实中的问题可没那么简单，主要的差别在于：

现实问题中，数据的维度非常多。

在预测成品率时，我们只考虑了温度这一个维度，在机器学习领域，这叫做一个“特征 (feature)”。

但假设我们要训练机器识别猫狗。一张 200 * 200 的图片就有 4 万个像素，每个像素又由 RGB 三个数值来决定颜色，所以一张图片就有 12 万个特征。换句话说，这个数据有 12 万个维度，这可比温度这一个维度复杂多了。好在，无论有多少个维度，数学逻辑是不变的。

现实问题中，数据之间不是线性关系。

在今天的例子中，成品率和温度之间是线性关系。但你可以想象得到，猫照片的 4 万个像素和“猫”这个概念之间，可不会是简单的线性关系。事实上两者之间的关系是如此复杂，只有用多层神经网络的上百万个参数（上百万个不同的 w：w1， w2，……w1000000）才足以表达。所谓“深度”学习指的就是这种多层网络的结构。

说到这里，我们可以回答前面的问题了：机器所学到的“知识”到底是什么？

就是这些w。

在今天的例子中，机器找到了正确的 w 值，所以当我们输入某一温度时，它能预测成品率。同样的，如果机器找到一百万个正确的 w 值，你给它看一张照片，它就能告诉你这是猫还是狗。

正因为现实问题如此复杂，为了提高机器学习的速度和效果，在实际的开发中，大家用的都是梯度下降的各种强化版本，但原理都是一样的。

深度学习是个日新月异的广袤领域，希望这个介绍能稍稍掀开机器学习的神秘面纱，给你一个看待“知识”的新角度。